New paper is live on arXiv:2112.14280!
For a quick summary, see this conference poster.
Whether or not a system is in a topological state seem mutually exclusive. We overturn this intuition: we introduce and analyze a situation where topologically distinct states exist in a quantum superposition.
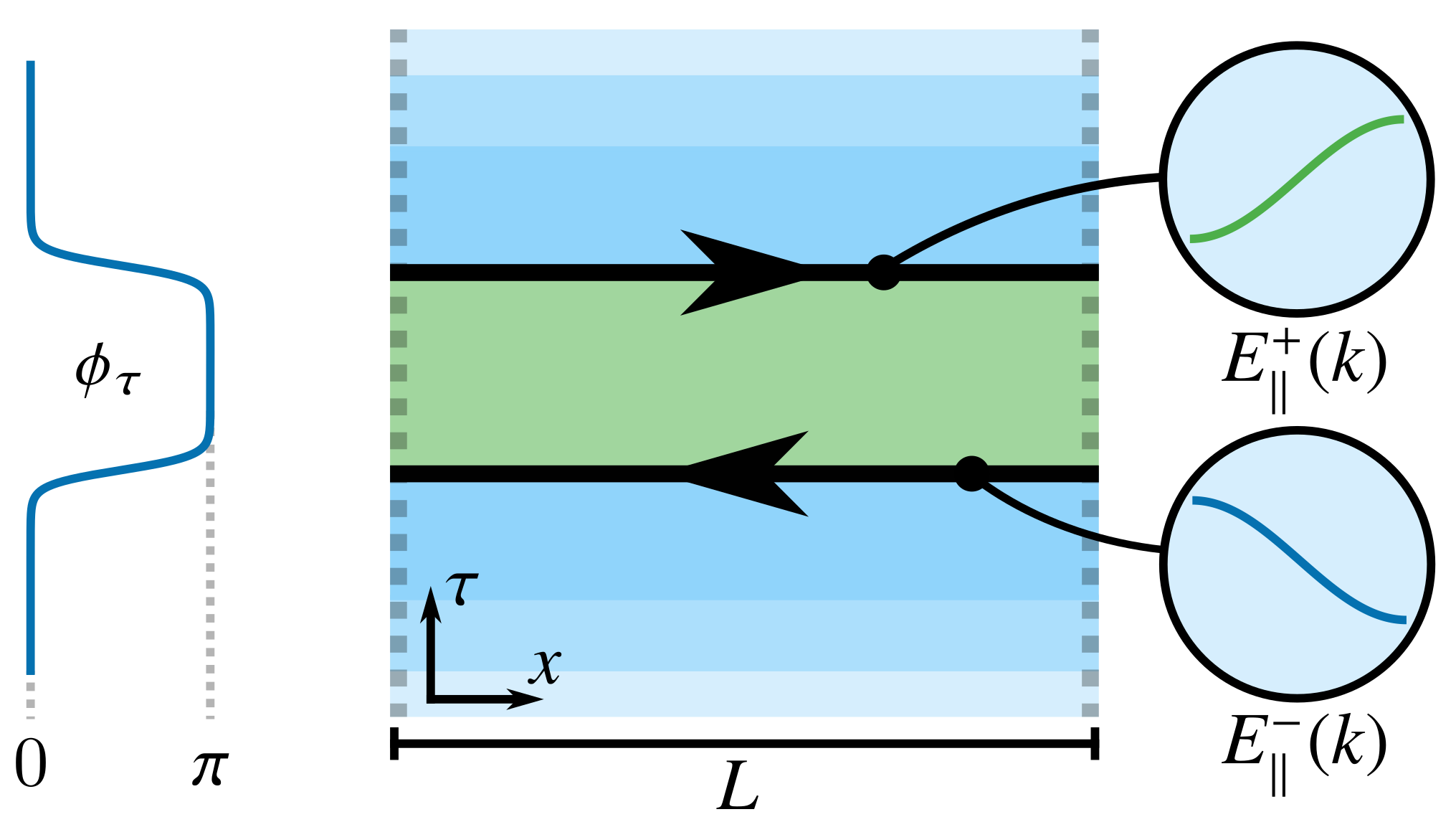
While a conceptual advance, our study is inspired by experiments: The prospects of Coulomb effects in recently created planar Josephson junction Majorana systems. To assess the conditions for topological superpositions, we study tunneling between topologically distinct states, including developing an instanton-based reversal of dimensional reduction and a numerical instanton technique to obtain accurate tunneling amplitudes for our many-body systems.
This work was completed under the supervision of Jan Behrends and Benjamin Béri. The abstract is copied and pasted below:
Coupling a quantum particle to a fermionic bath suppresses the particle’s amplitude to tunnel, even at zero temperature. While this effect can generally be neglected for gapped baths—a key feature for superconducting qubits—, it is possible for the bath to be gapped near the potential minima between which the particle tunnels, but different minima to correspond to different bath topologies. This enforces the bath to undergo gap closing along the tunneling path. In this work, we investigate quantum tunneling in the presence of such a topology-changing fermionic bath. We develop a field theory for this problem, linking the instantons describing tunneling in a bath of d space dimensions to topological boundary modes of systems in \( d+1 \) dimensions, thus stepping a level higher in a dimensional hierarchy. We study in detail a \( d=1 \) example, inspired by planar Josephson junctions where the particle coordinate is the superconducting phase whose value sets the electronic topology. We find that the topology change suppresses tunneling by a factor scaling exponentially with the system size. This translates to a correspondingly enhanced suppression of the energy splitting for the lowest-lying states, despite these being linear combinations of states near potential minima where the bath is gapped. Our results help to estimate the influence of charging energy on topological phases arising due to the Josephson effect and, conversely, to assess the potential utility of such topological systems as superconducting qubits. For moderate-sized baths, the incomplete suppression of tunneling opens the prospects of quantum-mechanical superpositions of many-body states of different topology, including superpositions of states with and without Majorana fermions.